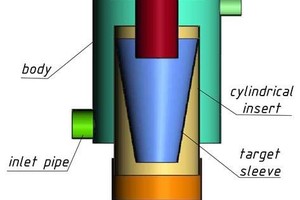
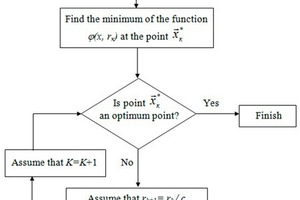
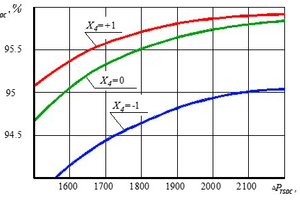
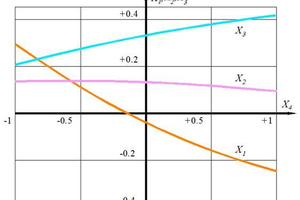
Optimization of the two-stage cyclone-type dust concentrator –
design and operating parameters
This article presents experimental research results data and optimization of a two-stage cyclone-type dust concentrator and the design and operating parameters data. To resolve the assigned optimization task, SUMT (Sequential Unconstrained Minimization Technique) was applied. The Davidon-Fletcher-Powell method was used to find the minimum of a function, afterwards the iterative procedure was realized. The results were processed using joint analysis of the characteristic curve with regression equation of dust collecting efficiency and liquid resistance.
1 Introduction
A large part of the technological processes of building materials enterprises, as well as a number of other branches of industry are the mechanical manipulation and material handling processes, related to the gravity flow of large amounts of granular materials on closed gutters and accompanied by intensive release of dust.
Traditional aspiration systems, characterized by volumetric emission of dusty air, are widely used for localization of sources of dust emissions. Reduction of the power consumption and the dust emission of the system can be achieved as a result of purification...